Bspline
Bspline上任意点的计算公式
Bspline和贝塞尔曲线类似，也是将所有控制点用基函数\(N_{i}^{k}\)进行加权得到曲线上的点。也就是说，Bspline有\(n+1\)个控制点，\(n+1\)个基函数，\(k\)为次数（t在基函数中出现的最高次幂），\(i\in[0,n]\)。比如有10个控制点\(p_0,p_1,p_2,p_3,...,p_{9}\)，使用4次的Bspline基函数\(N^{4}_{0}(t),N^{4}_{1}(t),N^{4}_{2}(t),N^{4}_{3}(t),...,N^{4}_{9}(t)\)，那么曲线上任意一点可以表示为：
\[ \begin{align*} f(t)&=\sum_{i=0}^{n}N_{i}^{k}(t)p_i\\ &=N_{0}^{4}p_0+N_{1}^{4}p_1+N_{2}^{4}p_2...+N_{9}^{4}p_{9}\tag{1} \end{align*} \]
节点
与贝塞尔曲线不同的是，Bspline除了控制点，基函数之外还有\(m+1\)个节点\(t_0,t_1,...,t_m\)。B样条基函数是分段k阶（k-1次）多项式，它们由节点向量(knot vector)唯一决定。\(n\)和\(m,k\)有如下关系：
\[ m=n+k\tag{2} \]
注意这里的k是指基函数中t的最高次幂而不是阶数，最高次幂为0时，阶数为1。如果阶数是k+1，那么关系为\(m=n+k+1\)。给出公式后就可以解释为什么有这个关系。
也就是说，在上面这个例子里，\(m=9+4=13\)，节点个数是14。为了方便理解，我们可以认为节点是用来生成基函数的辅助量。节点向量则是一串非减(non-decreasing)的实数序列，比如\([0,0,\frac{1}{11},\frac{2}{11},\frac{3}{11},\frac{4}{11},\frac{5}{11},\frac{6}{11},\frac{7}{11},\frac{8}{11},\frac{9}{11},\frac{10}{11},1,1]\)。一般来说节点的值是在\([0,1]\)之间，但是也可以不是。
Bspline基函数的定义
有了节点就可以计算基函数了，基函数的公式是递归定义的：
\[ N_{j}^{0}(t):=\left\{ {\begin{matrix}1&\quad t_{j}<t<t_{ {j+1} }\\0& {...}\end{matrix} }\right.\\ N_{j}^{k}(t):={\frac {t-t_{ {j} }}{t_{ {j+k} }-t_{j} }}N_{j}^{k-1}(t)+{\frac {t_{ {j+k+1} }-t}{t_{ {j+k+1} }-t_{ {j+1} }} }N_{j+1}^{k-1}(t).\tag{3} \]
看起来比较复杂，实际上从中可以看出对于节点\(t_j\)的几个特点：
- 0次的时候是一个仅在\([t_j,t_{j+1}]\)区间为1，其他地方的值为0的0次函数。从递归形式可以看出递归次数和次幂相同。
- \(k\)阶的基函数是由\(k-1\)阶的第\(j\)和\(j+1\)个基函数决定的。而且前一个基函数的权重是正的，后一个是负的（前一个t是正号，后一个的t是负号）。
- 从第一点可以看出0次的时候每个\(t_j\)分别在各自的\([t_j,t_{j+1}]\)上是1，其他地方是0。结合1，2点可以看出，\(f(t)\)在\([t_0,t_{m+1}]\)上不为0，其他位置为0。\(N_j^k (t)\)是\([t_j,t_{j+k} ]\)上的分段非零多项式。
- 随着\(N\)的次数（上标）增加到\(k\)，第\(j\)个节点的值受到第\(j\)到\(j+k\)个节点的值的影响。这个特点结合来自曲线篇：深刻理解B 样条曲线（上）的下图看更直观。
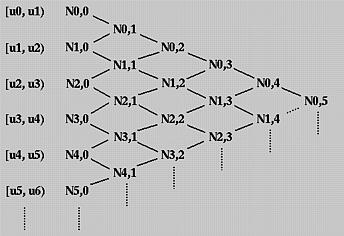
因为只有\(N_j^{k}(t)\)不为0时第\(j\)个控制点才有对计算贡献。从第四个特点可以得到一个重要的观察：在\([t_j,t_{j+k+1}]\)这个区间上第\(j\)个控制点才会用上，即Bspline具有局部性：每个控制点仅在\([t_j,t_{j+k+1}]\)内对曲线的形状有影响。若n非常小，改变了一个控制点的位置，影响的范围也是非常小的。
该图中还可以得到另一个重要的观察：当我们使用\(k\)次的基函数计算公式\((1)\)时，区间\([t_j,t_{j+1}]\)上仅有\(N_{j-k}^k,...,N_{j}^k\)有贡献，也就是说，这个区间上的曲线的形状由\(k\)个控制点决定。
上面的两个观察可以概括为Bspline的局部支持性：
- 区间\(t\in[t_j,t_{j+1}]\)上的曲线仅由至多k个控制点决定。
- 修改控制点\(p_i\) 仅会影响到区间\([t_j,t_{j+k+1}]\)上的曲线。
这里就可以解释为什么\(m=n+k\)。因为我们计算曲线上的点使用了公式\((1)\)，它需要\(N_{0}^{k},N_{1}^{k},...,N_{n}^{k}\)。但是从\(N_{0}^{0},...,N_{m}^{0}\)开始递归，每一次递归都会少一项，因为\(N_{m}^{1}\)只能由\(N_{m}^{1},N_{m+1}^{1}\)得到，但是\(N_{m+1}^{1}\)不存在，所以实际上当计算到\(k=1\)时，只能计算到\(N_{0}^{1},...,N_{m-1}^{1}\)。以此类推，计算到\(k\)时，只能计算到\(N_{0}^{k},...,N_{m-k}^{k}\)，最后的这一项就对应\(N_{n}^{k}\)。
在下面这个例子中，有四个控制点，最高三次，即\(k=3,n=3\)，总共6个节点。图中只画出部分基函数的曲线。
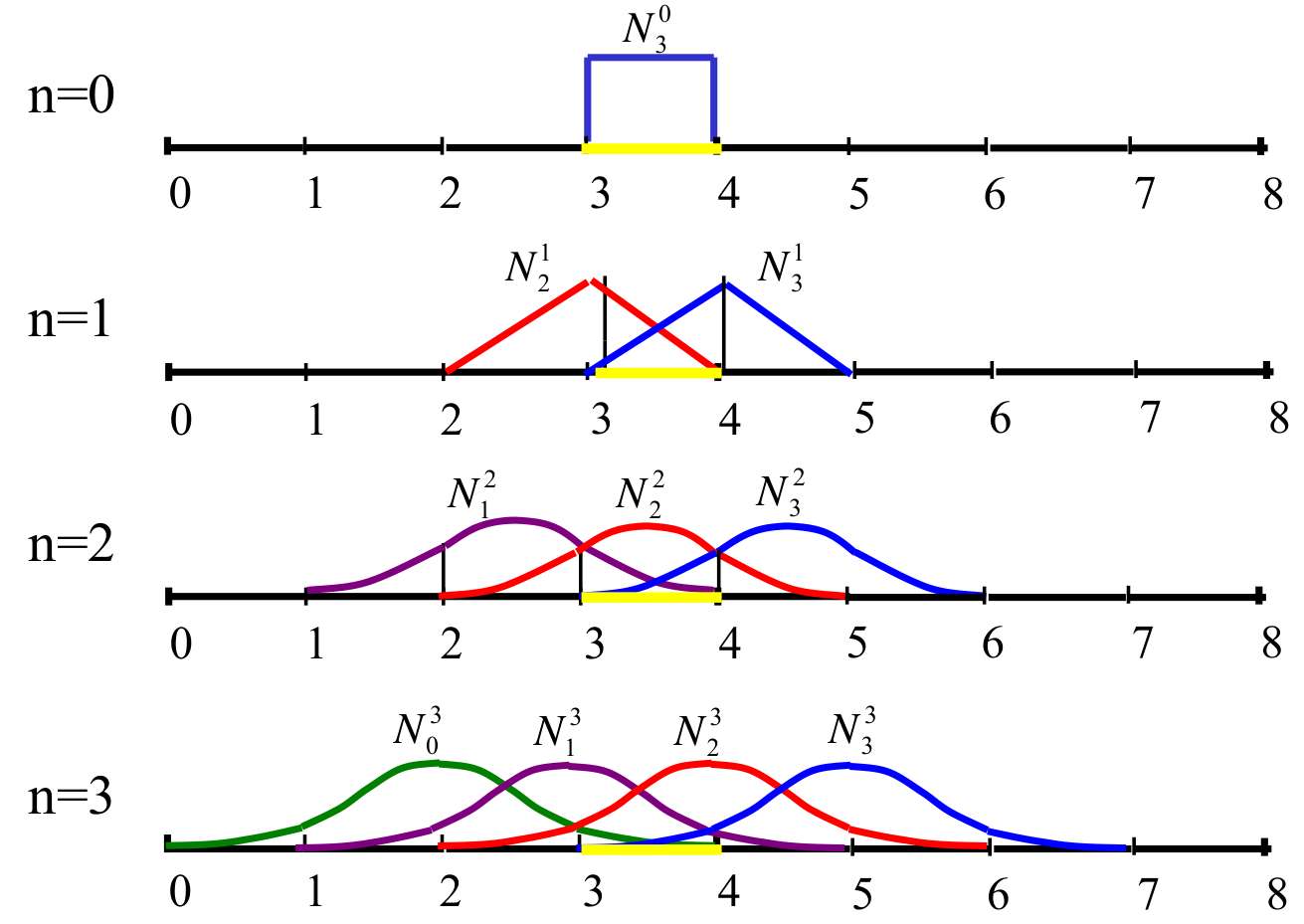从图中可以看到，同一个颜色的曲线对应着同一个序号\(j\)的\(N_j^k(t)\)，他们的左端点都是不变的，因为\((2)\)公式左端始终乘的是\(t-t_j\)，也就是说\(t=t_j\)时的值一定为0。
Bspline插值
已知\(m+1\)个点\((t_0,p_0),...,(t_m,p_m)\)，计算一条穿过所有点的Bspline的公式\(f(t)\)。
因为\(f(t)\)需要在\(t\in[t_j,t_{j+1}]\)上有定义，需要左右各增加\(k\)（次数）个节点。所有要确定节点向量\([\lambda_0,...\lambda_{m+2k}]\)，为方便计算，节点向量均匀分布，为
\[ \begin{align*} \mathbf{\lambda}&=\begin{bmatrix} t_{-3}&t_{-2}&t_{-1}& \vdots& t_0 &... &t_{m} &\vdots&t_{m+1}&t_{m+2}&t_{m+3}\end{bmatrix}\\ &=\begin{bmatrix} \lambda_{0}&\lambda_{1}& \lambda_2 &... &\lambda_{m+2n}\end{bmatrix} \end{align*} \]
由此可以计算矩阵\(\mathbf{A}\)。
For the cubic case \((k = 3)\) with natural spline endpoint conditions (i.e. second derivative = 0 at \(t_0\) and \(t_m\))。
\[ \mathbf{A}=\begin{bmatrix} { }^{(2)} N_0^3(t_0)& { }^{(2)} N_1^3(t_0)& { }^{(2)} N_2^3(t_0)& { }^{(2)} N_3^3(t_0)\\ N_0^3(t_0) & N_1^3(t_0) & N_2^3(t_0) & N_3^3(t_0)\\ & N_1^3(t_1) & N_2^3(t_1) & N_3^3(t_1) & N_4^3(t_1)\\ & & N_2^3(t_2) & N_3^3(t_2) & N_4^3(t_2) & N_5^3(t_2)\\ \\ & &\ddots& & \ddots & \ddots & &\\ \\ & & N_{m-3}^3(t_{m-3}) & N_{m-2}^3(t_{m-3}) & N_{m-1}^3(t_{m-3}) & N_m^3(t_{m-3}) \\ & & &N_{m-2}^3(t_{m-2}) & N_{m-1}^3(t_{m-2}) & N_m^3(t_{m-2}) & N_{m+1}^3(t_{m-2}) \\ & & & & N_{m-1}^3(t_{m-1}) & N_m^3(t_{m-1}) & N_{m+1}^3(t_{m-1}) & N_{m+2}^3(t_{m-1}) \\ & & & & N_{m-1}^3(t_m) & N_m^3(t_m) & N_{m+1}^3(t_m) & N_{m+2}^3(t_m) \\ & & & & { }^{(2)} N_{m-1}^3(t_m) &{ }^{(2)} N_m^3(t_m) &{ }^{(2)} N_{m+1}^3(t_m) & { }^{(2)} N_{m+2}^3(t_m) \\ & \end{bmatrix} \]
当\(k=3\)时，矩阵\(\mathbf{A}\)为\((m+3)\times(m+3)\)。
向量\(d=\begin{bmatrix}0 &p_0&p_1&...&p_m&0\end{bmatrix}\)。
求得系数为：
\[ c=\mathbf{A}^{-1}d,\\ \]
则可以得到Bspline的公式：
\[ f(t)=\sum_{j=0}^{m+k-1}c_jN_j^k(t) \]