Applications of eigenvectors

很多时候需要把已有问题转化为特征值问题。

1. 有一个对称矩阵（有时候是对称半正定矩阵），我们想要找一个方便的基。
2. 具体的优化问题。

Setup

Given: Collection of data points \(x_i\)

• Age
• Weight
• Blood pressure
• Heart rate

Find: Correlations between different dimensions

Simplest Model

One-dimensional subspace:

\[ \mathbf{x_i} \approx c_i \mathbf{v}, \quad \mathbf{v} \text{ unknown} \]

Equivalently:

\[ \mathbf{x_i} \approx c_i \hat{\mathbf{v}}, \quad \hat{\mathbf{v}} \text{ unknown with } ||\hat{\mathbf{v}}||_2 = 1 \]

Variational Idea

\[ \text{minimize } \sum_{i=1}^n ||\mathbf{x_i} - \text{proj}_{\hat{\mathbf{v}}} \mathbf{x_i}||_2^2\\ \text{subject to } ||\hat{\mathbf{v}}||_2 = 1 \]

What does the constraint do?

• Does not affect optimal \(\hat{\mathbf{v}}\).
• Removes scaling ambiguity.

Geometric Interpretation

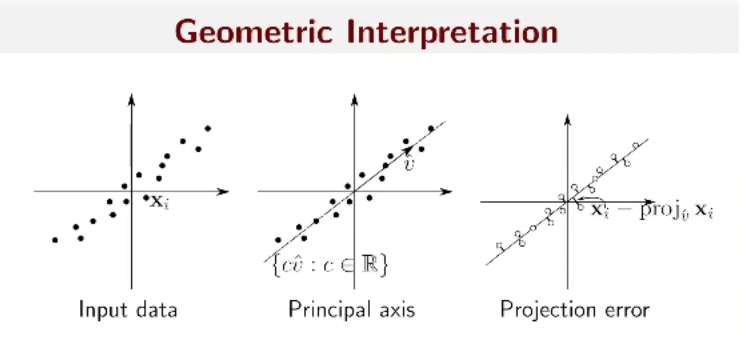
Review from Last Lecture

\[ \begin{aligned} &\min_{c_i} \sum_i ||\mathbf{x_i} - c_i \hat{\mathbf{v}}||_2^2 \\&\xRightarrow {c_i = \mathbf{x_i}\cdot \hat{\mathbf{v}}} \sum_i ||\mathbf{x_i} - (\mathbf{x_i}\cdot \hat{\mathbf{v}}) \hat{\mathbf{v}}||_2^2\\ &= \sum_i ||\mathbf{x_i}||_2^2 - 2 \sum_i (\mathbf{x_i}\cdot \hat{\mathbf{v}})^2 + \sum_i (\mathbf{x_i}\cdot \hat{\mathbf{v}})^2\\ &= \sum_i ||\mathbf{x_i}||_2^2 - \sum_i (\mathbf{x_i}\cdot \hat{\mathbf{v}})^2\\ &= \text{const.} - \sum_i (\mathbf{x_i}\cdot \hat{\mathbf{v}})^2\\ &= \text{const.} - ||X^T \hat{\mathbf{v}}||_2^2 \\ &= \text{const.} - \hat{\mathbf{v}}^T X X^T \hat{\mathbf{v}}, \end{aligned} \]

\[ X=\begin{bmatrix} | & | & & | \\ \mathbf{x_1} & \mathbf{x_2} & \cdots & \mathbf{x_n} \\ | & | & & | \end{bmatrix}\\ \]

\[ X^T \hat{\mathbf{v}} = \begin{bmatrix} \mathbf{x_1}\cdot \hat{\mathbf{v}} \\ \mathbf{x_2}\cdot \hat{\mathbf{v}} \\ \vdots \\ \mathbf{x_n}\cdot \hat{\mathbf{v}} \end{bmatrix} \]

Equivalent Optimization

\[ \textrm{maximize } ||X^T \hat{\mathbf{v}}||_2^2\\ \textrm{subject to } ||\hat{\mathbf{v}}||_2 = 1 \]

homogeneous quadratic function with quadratic constraint，有二次约束（尤其是norm为1）的齐次二次优化问题，可以转化为特征值问题。

\[ \Lambda(\hat{\mathbf{v}};\lambda) = \frac{1}{2} \hat{\mathbf{v}}^T X X^T \hat{\mathbf{v}} + \lambda (\frac{1}{2} - \frac{1}{2} ||\hat{\mathbf{v}}||_2^2)\\ \mathbf{0} = \nabla_{\hat{\mathbf{v}}} \Lambda(\hat{\mathbf{v}};\lambda) = X X^T \hat{\mathbf{v}} - \lambda \hat{\mathbf{v}}\\ \Rightarrow X X^T \hat{\mathbf{v}} = \lambda \hat{\mathbf{v}}\\ \]

\[ \mathbf{v} X X^T \hat{\mathbf{v}} = \lambda \mathbf{v} \hat{\mathbf{v}} = \lambda\\ \] 因此最优的\(\hat{\mathbf{v}}\)是\(X X^T\)的最大的特征值对应的特征向量。

End Goal

Eigenvector of \(X X^T\) with largest eigenvalue.

"Firs principal component"

More after SVD.

问题转化

\[ \min \frac{1}{2} x^T A x - x^T b \rightarrow Ax = b\\ \min \frac{1}{2} x^T A x \text{ s.t. } ||x||_2^2 = 1 \rightarrow Ax = \lambda x, A \text{ positive semidefinite} \]

Physics

Newton:

\[ \mathbf{F} = m \frac{d^2 \mathbf{x}}{dt^2} \]

Hooke:

\[ \mathbf{F} = -k (\mathbf{x}-\mathbf{y}) \]

\[ \mathbf{F}\in \mathbb{R}^{3n}, \mathbf{X} \in \mathbb{R}^{3n}\\ \mathbf{F}=M\mathbf{X}''=A\mathbf{x}\\ v:=x' \]

\[ \frac{d}{dt} \begin{bmatrix} \mathbf{x} \\ \mathbf{v} \end{bmatrix} = \begin{bmatrix} \mathbf{0} & I_{3n \times 3n}\\ M^{-1}A & \mathbf{0} \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ \mathbf{v} \end{bmatrix} \]

General Linear ODE

\(\mathbf{y}\)是关于时间的向量值函数，\(\mathbf{y}_i\)是\(B\)的特征向量，\(\lambda_i\)是特征值。 \[ \mathbf{y}' = B \mathbf{y} \\ B \mathbf{y}_i = \lambda_i \mathbf{y}_i\\ \]

可以假设： \[ \mathbf{y}(0)= c_1 \mathbf{y}_1 + c_2 \mathbf{y}_2 + \cdots + c_k \mathbf{y}_k\\ \] 此外，假设\(\mathbf{y}_i\) span \(\mathbb{R}^n\)，则： \[ \mathbf{y}(t) = \sum_{i=1}^n c_i(t) \mathbf{y}_i\\ B\mathbf{y} = \sum_{i=1}^n c_i(t) B \mathbf{y}_i = \sum_{i=1}^n c_i(t) \lambda_i \mathbf{y}_i\\ \mathbf{y}'(t) = \sum_{i=1}^n c_i'(t) \mathbf{y}_i\\ \] 因为\(B\mathbf{y} = \mathbf{y}'\): \[ c_i'(t) = \lambda_i c_i(t)\\ \rightarrow c_i(t) = c_i(0) e^{\lambda_i t}\\ \mathbf{y}(t) = c_1 e^{\lambda_1 t} \mathbf{y}_1 + c_2 e^{\lambda_2 t} \mathbf{y}_2 + \cdots + c_k e^{\lambda_k t} \mathbf{y}_k\\ \]

Linear Systems

\[ \mathbf{b} = c_1 \mathbf{x}_1 + c_2 \mathbf{x}_2 + \cdots + c_k \mathbf{x}_k\\ A \mathbf{x} = \mathbf{b}\\ \Rightarrow \mathbf{x} = \frac{c_1}{\lambda_1} \mathbf{x}_1 + \frac{c_2}{\lambda_2} \mathbf{x}_2 + \cdots + \frac{c_k}{\lambda_k} \mathbf{x}_k\\ \]

Verify:

\[ A \mathbf{x} = \sum_{i=1}^k \frac{c_i}{\lambda_i} A \mathbf{x}_i = \sum_{i=1}^k \frac{c_i}{\lambda_i} \lambda_i \mathbf{x}_i = \sum_{i=1}^k c_i \mathbf{x}_i = \mathbf{b} \]

Organizing a Collection

Setup

Have: n items in a dataset

\(w_{ij} \geq 0\) similarity of items \(i\) and \(j\)

\(w_{ij} = w_{ji}\)

Want: \(x_i\) embedding on \(\mathbb{R}\)

我们希望\(w_{ij}\)越大，\(x_i\)和\(x_j\)越接近: \[ \min_{\{x_i\}} E(\mathbf{x}),\\ E(\mathbf{x}) = \sum_{i,j} w_{ij} (x_i - x_j)^2,\\ \text{s.t. } ||\mathbf{x}||_2^2 = 1 \leftrightarrow \sum_i x_i^2 = 1\\ \mathbf{1} \cdot \mathbf{x} = 0 \leftrightarrow \sum_i x_i = 0 \]

Let \(a:=w \cdot \mathbf{1}\),

\[ \begin{aligned} E(\mathbf{x}) &= \sum_{i,j} w_{ij} (x_i^2 - 2x_i x_j + x_j^2) \\ &= \sum_{i,j} w_{ij} x_i^2 - 2 \sum_{i,j} w_{ij} x_i x_j + \sum_{i,j} w_{ij} x_j^2\\ &= 2\sum_{i} a_i x_i^2 - 2 \sum_{i,j} w_{ij} x_i x_j\\ &= 2x^T A x - 2x^T W x\\ &= 2x^T (A - W) x, \end{aligned}\\ A=diag(a)\\ \]

Fact:

\[ (A-W) \mathbf{1} = diag(a) \mathbf{1} - W \mathbf{1} = a - a = 0 \]

Lagrange multiplier:

\[ \Lambda = 2x^T (A-W) x - \lambda (x^T x - 1) - \mu (\mathbf{1}^T x)\\ \Rightarrow \nabla_x \Lambda = 4(A-W)x - 2 \lambda x - \mu \mathbf{1} = 0\\ \]

Premultiply by \(\mathbf{1}^T\) on both sides:

\[ \begin{aligned} &\mathbf{1}^T 4(A-W)x - \mathbf{1}^T 2 \lambda x - \mathbf{1}^T \mu \mathbf{1} \\ &= 4 \mathbf{1}^T (A-W)x - 2 \lambda \mathbf{1}^T x - \mu n \\ &= 0 - 0 - \mu n = 0\\ &\Rightarrow \mu = 0 \end{aligned}\\ \therefore \Lambda = 0 \Rightarrow 2(A-W)x = \lambda x\\ E(\mathbf{x}) = x^T (A-W) x = x^T \lambda x = \lambda x^T x = \lambda \]

\(\mathbf{x}\) is eigenvector of \(A-W\) with smallest \(\lambda\not=0\).

\(\lambda\) 不为0的原因是\(E(\mathbf{x})\)不能为0，否则所有的\(x_i\)相等，与约束条件矛盾。

Definition

Eigenvalue and eigenvector

An eigenvector \(\mathbf{x}\not=0\) of \(A \in \mathbb{R}^{n \times n}\) satisfies \(A \mathbf{x} = \lambda \mathbf{x}\) for some \(\lambda \in \mathbb{R}\); \(\lambda\) is an eigenvalue. Complex eigenvalues and eigenvectors instead have \(\lambda \in \mathbb{C}\) and \(x \in \mathbb{C}^n\).

Scale doesn't matter!

\(\rightarrow\) can constrain \(||\mathbf{x}||_2 = 1\).

Spectrum and spectral radius

The spectrum of \(A\) is the set of all eigenvalues of \(A\). The spectral radius \(\rho(A)\) is the maximum value \(|\lambda|\) over all eigenvalues \(\lambda\) of \(A\).

Eigenproblems in the Wild

• Optimize \(A\mathbf{x}\) subject to \(||\mathbf{x}||_2 = 1\).(important!)
• ODE/PDE problem: Closed solutions and approximations for \(\mathbf{y}' = B \mathbf{y}\).
• Critical points of Rayleigh quotient: \(\frac{\mathbf{x}^T A \mathbf{x}}{||\mathbf{x}||_2^2}\).