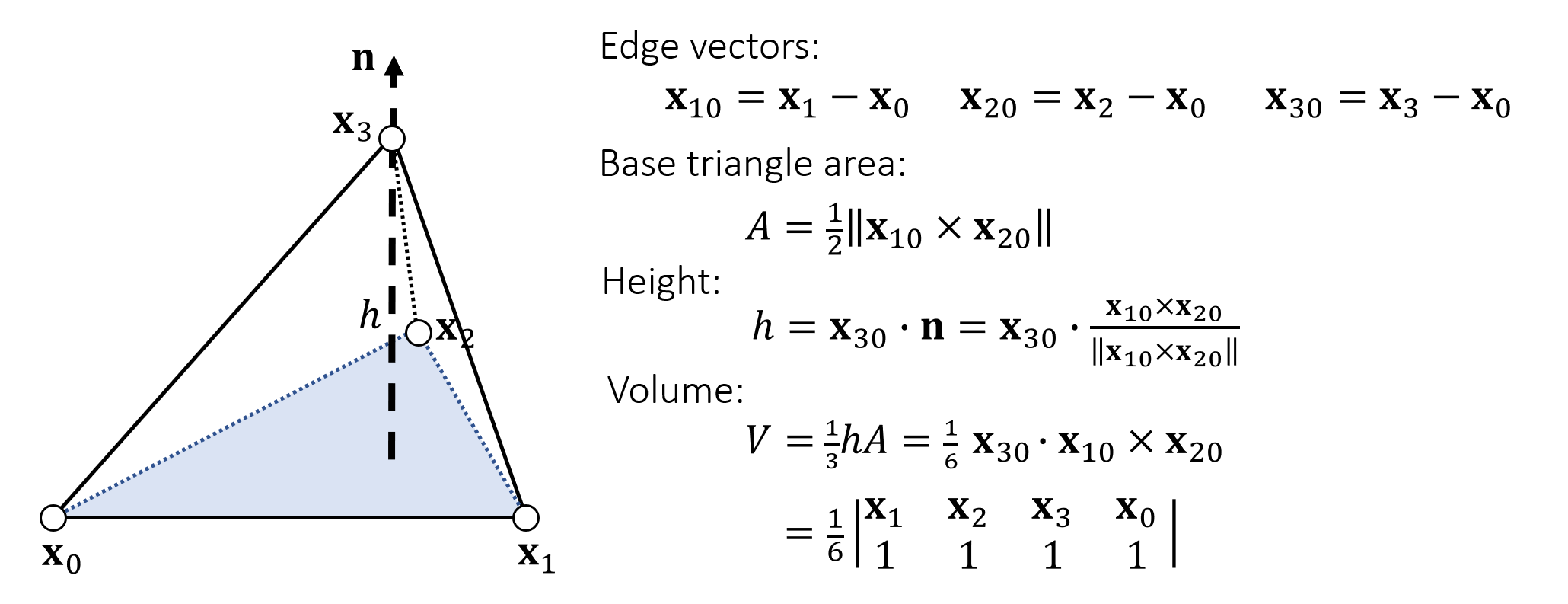
在进行软体模拟时，如果使用牛顿法计算最优的下降方向，需要计算能量密度函数\(\Psi\)关于位置\(\vec {\mathbf{x}}\) 的Hessian矩阵，即\(\frac{\partial^2 \Psi}{\partial \vec {\mathbf{x}}^2}\)。其中\(\vec {\mathbf{x}}\)是一个四面体的四个顶点的位置。
\[ \begin{equation} \frac{\partial^2 \Psi}{\partial {\mathbf{x}^2}} = \text{vec}(\frac{\partial F}{\partial {\mathbf{x}}})^T \text{vec}(\frac{\partial P}{\partial F}) \text{vec}(\frac{\partial F}{\partial {\mathbf{x}}}) \end{equation} \]
首先，已知
\[ \vec {\mathbf{x}} = \begin{bmatrix} \vec x_1 & \vec x_2 & \vec x_3 \end{bmatrix}\\ D_s = \begin{bmatrix} \vec x_1-\vec x_4 & \vec x_2-\vec x_4 & \vec x_3-\vec x_4 \end{bmatrix}\\ \begin{aligned} &\frac{\partial (D_s)_{kl}}{\partial \vec {\mathbf{x}_{ij}}} e_i\otimes e_j\otimes e_k\otimes e_l\\ &=\frac{\partial \vec {\mathbf{x}}_{kl}}{\partial \vec {\mathbf{x}}_{ij}} e_i\otimes e_j\otimes e_k\otimes e_l\\ &= \delta_{ik}\delta_{jl} e_i\otimes e_j\otimes e_k\otimes e_l \end{aligned} \] 这里把\(\vec {\mathbf{x}}\)后三列写成一个3x3的矩阵。\(D_m^{-1}\)的分量表示为\(d_{mn}\)，\(P\)的分量表示为\(P_{rs}\)，则能量密度函数\(\Psi\)关于位置\(\vec {\mathbf{x}}\) 的梯度为：
Projective Dynamics是一种用于软体模拟的方法，算法分为local step和global step两个部分。其中local step可以对于每个四面体约束并行计算，global step只需要求解一个线性方程组，而他的矩阵非常特殊，是一个Gram矩阵，因此可以预先用Cholesky分解。本文主要介绍local step的实现的推导过程。用Corotated strain model的CUDA的实现作为例子。
