Hermite插值多项式

Hermite插值是一种插值方法，可以通过给定的点和导数值构造插值多项式。给定点$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$和导数值$y'_0,y'_1,...,y'_n$，可以构造插值多项式。本文介绍如何使用Newton差商生成Hermite插值多项式。

介绍

该文章中的c++代码参考了ipc-toolkit的实现。

点到三角形的距离可以用如下定义：

$$\begin{aligned} \text{distance}(\vec{\mathbf{x_p}}, \vec{\mathbf{x_t}_1}, \vec{\mathbf{x_t}_2}, \vec{\mathbf{x_t}_3}) &= \min_{\beta_1, \beta_2} \left\| \vec{\mathbf{x_p}} - ( \vec{\mathbf{x_t}_1} + \beta_1 (\vec{\mathbf{x_t}_2} - \vec{\mathbf{x_t}_1}) + \beta_2 (\vec{\mathbf{x_t}_3} - \vec{\mathbf{x_t}_1}) ) \right\| \\&s.t. \beta_1 \geq 0, \beta_2 \geq 0, \beta_1 + \beta_2 \leq 1 \end{aligned}$$

这是一个分断连续的函数，实际计算时可以根据点和三角形的位置关系分以下几种情况讨论，首先要将点投影到三角形所在的平面上：

1. 投影后，点在三角形内部，此时距离为点到三角形所在平面的距离。
2. 投影后，点在三角形的某个边朝外的半平面且投影在边上的点在边上，此时距离为点到边的距离。
3. 其他情况，此时距离为点到三角形的三个顶点的最小距离。

介绍

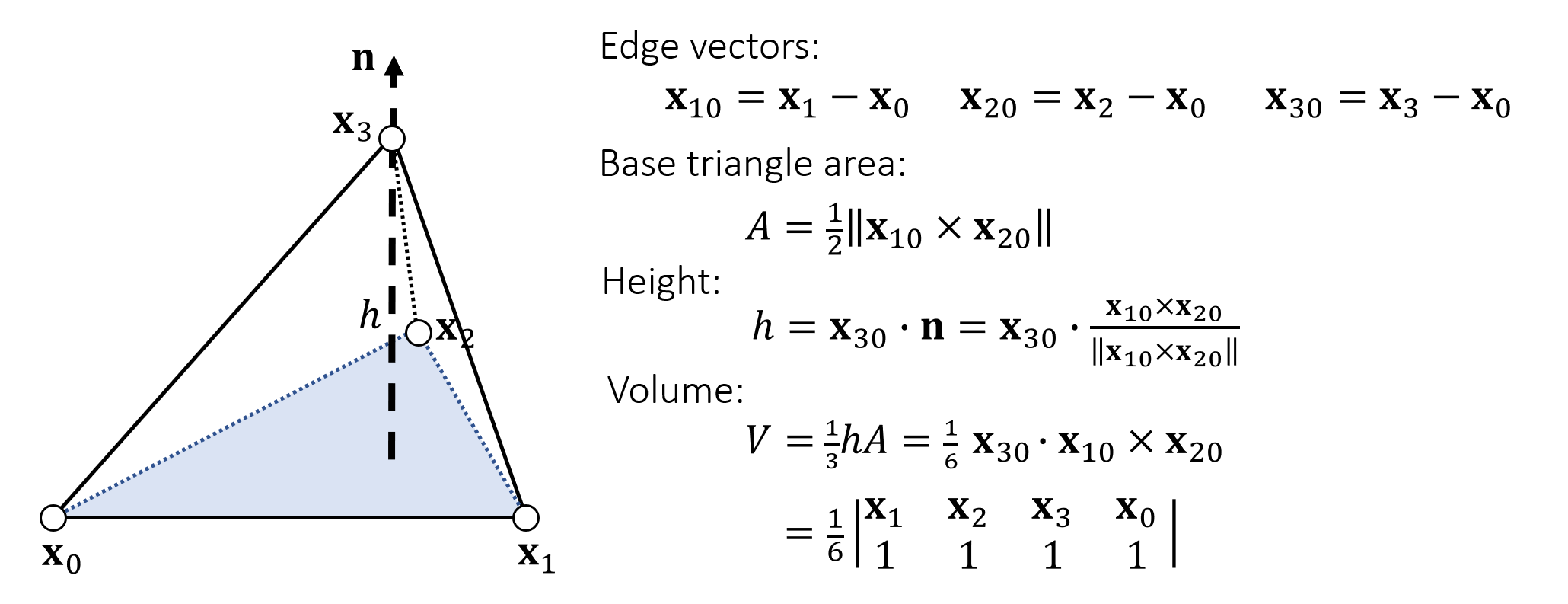
在进行软体模拟时，如果使用牛顿法计算最优的下降方向，需要计算能量密度函数$\Psi$关于位置$\vec {\mathbf{x}}$ 的Hessian矩阵，即$\frac{\partial^2 \Psi}{\partial \vec {\mathbf{x}}^2}$。其中$\vec {\mathbf{x}}$是一个四面体的四个顶点的位置。

$$\begin{equation} \frac{\partial^2 \Psi}{\partial {\mathbf{x}^2}} = \text{vec}(\frac{\partial F}{\partial {\mathbf{x}}})^T \text{vec}(\frac{\partial P}{\partial F}) \text{vec}(\frac{\partial F}{\partial {\mathbf{x}}}) \end{equation}$$

证明1

首先，已知

$$\vec {\mathbf{x}} = \begin{bmatrix} \vec x_1 & \vec x_2 & \vec x_3 \end{bmatrix}\\ D_s = \begin{bmatrix} \vec x_1-\vec x_4 & \vec x_2-\vec x_4 & \vec x_3-\vec x_4 \end{bmatrix}\\ \begin{aligned} &\frac{\partial (D_s)_{kl}}{\partial \vec {\mathbf{x}_{ij}}} e_i\otimes e_j\otimes e_k\otimes e_l\\ &=\frac{\partial \vec {\mathbf{x}}_{kl}}{\partial \vec {\mathbf{x}}_{ij}} e_i\otimes e_j\otimes e_k\otimes e_l\\ &= \delta_{ik}\delta_{jl} e_i\otimes e_j\otimes e_k\otimes e_l \end{aligned}$$ 这里把$\vec {\mathbf{x}}$后三列写成一个3x3的矩阵。$D_m^{-1}$的分量表示为$d_{mn}$，$P$的分量表示为$P_{rs}$，则能量密度函数$\Psi$关于位置$\vec {\mathbf{x}}$ 的梯度为：

介绍

Projective Dynamics是一种用于软体模拟的方法，算法分为local step和global step两个部分。其中local step可以对于每个四面体约束并行计算，global step只需要求解一个线性方程组，而他的矩阵非常特殊，是一个Gram矩阵，因此可以预先用Cholesky分解。本文主要介绍local step的实现的推导过程。用Corotated strain model的CUDA的实现作为例子。

2 Math

Tetrahedral Volume

1681077071804

Bspline上任意点的计算公式

光传播方程(The Light Transport Equation, LTE)

$$L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{s^2}f(p,\omega_o,\omega_i)|\cos\theta_i|d\omega_i$$

本来想写BSDF的推导，但是发现基础知识很多，正好整理一下作为复习。部分内容参考Physically Based Rendering, Third Edition，非常推荐阅读。

光线投射公式

从相机发出一条光线，穿过与相机距离为1的屏幕上的某点，已知相机参数和点在屏幕空间上的位置(sx,sy)，计算世界空间中投影到该点的对应点的坐标的公式为： $$P = ViewMat^{-1} * ProjMat^{-1} * ((sx, sy, 1, 1) * farClip).$$